Area of a trapezoid

Area A =

(b1 + b2) x h / 2

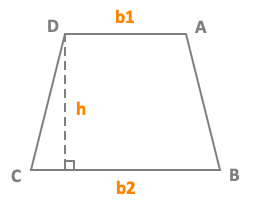
DA = base 1 = b1
CB = base 2 = b2
h = height

Example

ABCD is a trapezoid with a base b1 = 4 cm, a base b2 = 8 cm and a height h = 3 cm
Area A of a trapezoid ABCD =

(b1 + b2) x h / 2

(4 + 8) x 3 / 2

12 x 3 / 2

= 18 cm²

Calculate the area of a trapezoid

Definition of a trapezoid

A trapezoid is a quadrilateral that has 2 parallel sides.
A trapezoid, also known as a trapezium, is a flat shape with 4 straight sides that has a pair of opposite sides parallel.

The parallel sides of a trapezoid are called the bases of the trapezoid. In the general case where the quadrilateral has only one pair of parallel sides, these are called the small base and the large base.
The bases are parallel by definition.
A trapezoid is a quadrilateral with exactly one pair of parallel sides.
A trapezoid is called a trapezium in the UK.

To find the area of a trapezoid, multiply the sum of the bases by the height, and then divide by 2.
The area of a trapezoid is equal to half the product of the height and the sum of the two bases.

Properties of a trapezoid

The parallel sides of a trapezoid create the bases. The bases are parallel by definition.
Angles next to each other sum up to 180°. Each lower base angle of a trapezoid is supplementary to the upper base angle on the same side.

Isosceles trapezoid

An isosceles trapezoid (called an isosceles trapezium by the British) is a trapezoid whose legs are congruent. It is like an isosceles triangle.
An isosceles trapezoid is a quadrilateral having one pair of parallel sides and one pair of congruent legs. The bases (top and bottom) of an isosceles trapezoid are parallel and the opposite sides are congruent (the same length).
It has base angles which are congruent and diagonals which are congruent. The angles on either side of the bases are congruent (the same size).
The opposite angles of an isosceles trapezoid are supplementary. Indeed their sum is 180°. Adjacent angles (next to each other) along the sides of the isosceles trapezoid are supplementary (indeed their measures add up to 180°).

To go further

The bases (the top and bottom) are parallel to each other.
The base angles of an isosceles trapezoid are congruent.
A right trapezoid is a trapezoid with a right angle (90 degree)

Types of trapezoids

Isosceles trapezoid: when it has equal angles from a parallel side. An isosceles trapezoid is a trapezoid in which the base angles are equal and the left and right side lengths are also equal.
Right trapezoid: when it has two adjacent right angles (90°).
Scalene trapezoid: when neither the sides nor the angles of the trapezoid are equal, then it is a scalene trapezoid.
Obtuse trapezoid: when it has one interior angle (created by either base and a leg) greater than 90°.
Acute trapezoid: when it has two adjacent acute angles on its longer base edge.